Visualization Demo (Click to draw)

• run runs the algoirthm after data and centroids have been drawn.
• clear clears the screen and resets the data.
• Draw Centroids toggles centroid drawing mode.
• Draw Point toggles single point drawing mode.
• Draw Cluster toggles point cloud drawing mode. The number of points can be adjusted in the number input. The standard deviation can be adjusted by the slider.

Lloyd’s ( naïve K-Means) Algorithm

Basic Idea

The goal of the algorithm is to partition a dataset into $k$ clusters of data, hence the name KMeans. The algorithm iterates between two steps:

1. Data points are assigned to the nearest centroid
2. Centroids are updated based on the previous assignments.

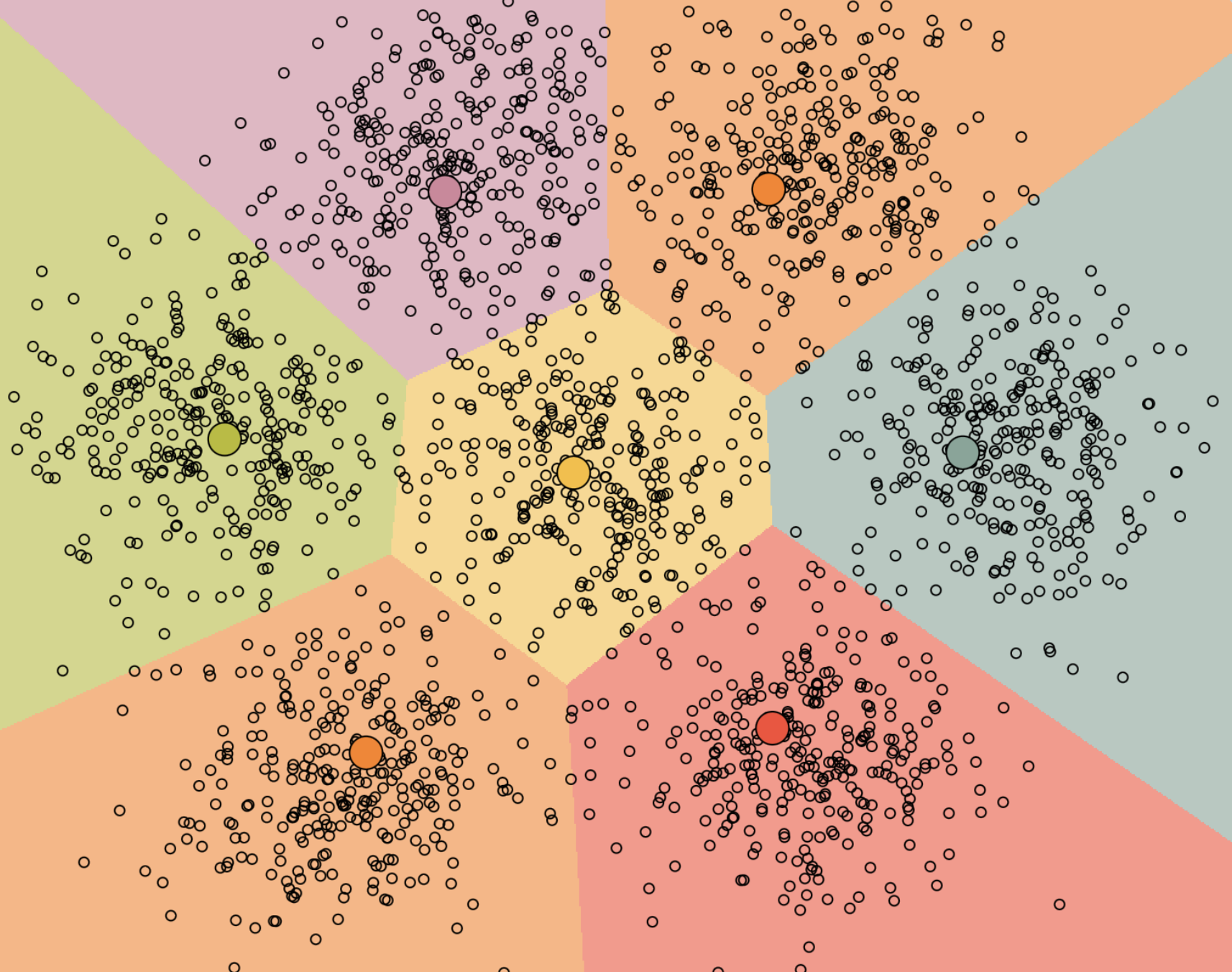
Formal Definition

More formally, given a set of observations $(\mathbf{x}_1, \mathbf{x}_2, \cdots, \mathbf{x}_n) \in \mathbb{R}^d$, the algorithm aims to partition the observations into $k \leq n$ sets $\mathbf{S} = ( S_1, S_2, \cdots, S_k )$ in order to minimize the within-cluster distances or sum of squares. Thus the objective becomes:

$$ \underset{\mathbf{S}}{\arg\min} \sum_{i=1}^{k} \sum_{\mathbf{x} \in S_i} \parallel \mathbf{x} - \mathbf{\mu}_i \parallel^2 $$

Here $\mu_i = \frac{1}{|S_i|} \sum_{x \in S_i} x$ and $|S_i|$ is the size of $S_i$.

The update steps becomes:

1. Assign each observation to the nearest mean (i.e. the mean with the least squared Euclidean distance).

$$ S_i^{(t)} = x_p : \parallel x_p - m_i^{(t)}\parallel^2 \leq \parallel x_p - m_j^{(t)}\parallel^2 \forall j, 1 \leq j \leq k$$

2. Recalculate the means based on the observations assigned to each cluster.

$$ \mu_i^{(t + 1)} \frac{1}{|S_i|} \sum_{x_j \in S_i^{(t)}} x_j $$

Lloyd’s algorithm is the standard approach for this problem. However, it spends a lot of processing time computing the distances between each of the $k$ cluster centers and the $n$ data points. Since points usually stay in the same clusters after a few iterations, much of this work is unnecessary, making the naïve implementation very inefficient. Some implementations use caching and the triangle inequality in order to create bounds and accelerate Lloyd’s algorithm.